Riddler Submission

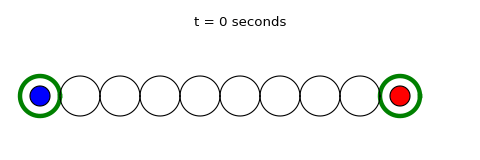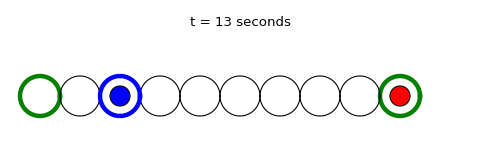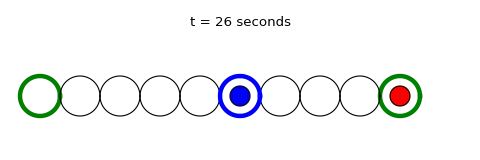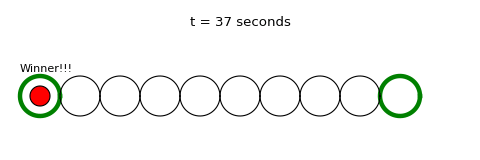
As you will come to notice throughout the course of this blog, I am a big fan of the website FiveThirtyEight and one weekly segment called The Riddler edited by Oliver Roeder. Every Friday, it challenges its readers to two math/probability/logic puzzles, one shorter, more accessible problem and one longer, more time-consuming problem for the hardcore puzzle nerds. It’s a fun way to end the week while stretching your brain and maybe picking up a computational tool or two while you’re at it.

After getting hooked and submitting answers for a few months, I started itching to submit a question for the Riddler community. It took a little while, but a problem worthy of this esteemed group came to me a couple of weeks ago, and much to my surprise, it was actually published! At the time, the following video of a unique schoolyard game had been making the rounds on Facebook and it seemed like a fun thing to model:

Idealized Rules of Rock-Paper-Scissors-Hop

• Kids stand at either end of N hoops.
• At the start of the game (t = 0), one kid from each end starts hopping at a speed of v = 1 hoop per second until they run into each other, either in adjacent hoops or if they land in the same hoop.
• At that point, they play rock-paper-scissors at a rate of 1 game per second until one of the kids wins.
• The loser goes back to their end of the hoops, a new kid steps up at that end, and the winner and the new player hop until they run into each other.
• This process continues until someone reaches the opposing end and that player wins!

Now, imagine you are a gym teacher having a bad day and you want to make sure the kids stay occupied for the entire class. If I put down 8 hoops, how long on average will the game last? How many hoops should I put down if I want the game to last for the entire 30 minute period on average?

Solution

Obviously, I had to have a solution in order to submit the problem, but I was flabbergasted at the kinds of the solutions that were submitted. Multiple solvers had code that was far more elegant than mine and the analytical solutions from Laurent Lessard and Tim Black (which cleverly involved a hyper-intelligent firefly) were mind-blowing. So please be warned ahead of time that my solution is not as pretty as those ones, but it still works… #AforEffort #YesIKnowHashtagsDontWorkInBlogs #OrDoThey

The easiest solution would probably be a Monte Carlo simulation. Mimicking the rules of the game, the code below advances players from either end until they meet in the middle. It then picks a random number to decide which player wins the rock-paper-scissors matchup and this repeats until either side reaches the other side. The time length of the game is recorded and then the entire game is repeated 10⁶ times to create a distribution of game lengths. My coding language of choice is Python, but this can easily been done using pretty much any language:

import numpy as np

numHoops = 8
leftWinProb = 1.0/3.0
rightWinProb = 1.0/3.0
hopTime = 1
rpsTime = 1

timeVals = []
for numTry in range(1000000):
	if (numTry + 1)%1000 == 0:
		print('Try #' + str(numTry + 1))
	timeVals.append(hopTime)
	leftPos = 0
	rightPos = numHoops - 1
	while rightPos - leftPos > 1:
		timeVals[-1] += hopTime
		leftPos += 1
		rightPos -= 1
	while leftPos < numHoops and rightPos >= 0:
		timeVals[-1] += rpsTime
		rockPaperScissors = np.random.rand()
		while rockPaperScissors >= leftWinProb + rightWinProb:
			timeVals[-1] += rpsTime
			rockPaperScissors = np.random.rand()
		timeVals[-1] += hopTime
		if rockPaperScissors < leftWinProb:
			leftPos += 1
			rightPos = numHoops - 1
		elif rockPaperScissors < leftWinProb + rightWinProb:
			leftPos = 0
			rightPos -= 1
		while np.all([rightPos - leftPos > 1,leftPos < numHoops,rightPos >= 0]):
			timeVals[-1] += hopTime
			leftPos += 1
			rightPos -= 1
del numTry

I also made an analytical solution that calculates the time and probability of every possible path of a game up to 99.9% of probability. It’s a bit of a “brute force” method and is definitely impractical for larger hoop numbers, but it gets the job done. Overlaying the distributions for an eight hoop game from simulations (orange trace) and the analytical method (blue trace) produces the figure to the right, and as you can see, things line up perfectly. These distributions suggest that an average eight hoop game would last 59.46 seconds, answering the first part of the original question. If we adjust the “numHoops” variable in the code, you can also find that it takes 57 hoops for a game to take more than thirty minutes on average, answering the second part of the original question. Just for kicks, you can also generate a sample gif of a single game (like the one at the top of this article) to demonstrate how the dynamics work! My answer may not be quite as elegant as the rest of Riddler Nation, but it was fun coming up with the question in the first place and I’m inspired by the originality of everyone’s answers. Thanks for tuning in! Hope everyone had fun!