Riddler Answer: Printers are from Mars, Scanners are from Venus

This week’s edition of the Riddler from Jerry Myers takes us to our rusty planetary neighbor and asks us to calculate the odds of our survival based on three (fairly unreliable) 3D printers. With Mars being a harsh environment, a vital piece of equipment will break exactly once per day and one of the printers must print a replacement part. However, each printer can only print one piece per day and they each have a 10%, 7.5%, and 5% chance respectively of breaking each day. Based on this less than ideal scenario, what are the odds that you would survive a 1825 day long journey?

Solution

If I understand the description of the scenario correctly, the only way you would die is if all three printers break in the same day because all other scenarios are fixable. For instance, if printers A and B both fail, printer C can print a part to fix printer B, printer B can then print a piece to fix printer A, and finally, printer A can then print a new part for the vital equipment. By this logic, the probability of surviving the entire journey would be

However, the problem gets much more interesting if we make it a bit more realistic. Specifically, we can make the vital equipment/printer failures a random process using a Gillespie algorithm like the one shown below. On average, one piece of vital equipment will still break each day and each printer will have the same odds of breaking each day, but there is now a significant chance of having multiple breakages in a single day. When anything breaks, the next available printer will print a replacement but then remain unavailable for the next 24 hours to recharge.

import numpy as np

printerLag = 1.0 # Number of days before a printer is ready to print again
numDays = 1825 # Number of days in your martian adventure
printerRates = np.array([0.05,0.075,0.1]) # Probabilities of each printer breaking
vitalRate = 1.0 # Rate at which vital equipment breaks (measured in malfunctions per day)
numSims = 10000 # Number of simulations to run before averaging

times = []
for numSim in range(numSims):
    if (numSim + 1)%1000 == 0:
        print('Try #' + str(numSim + 1))
    time = 0.0
    printers = np.ones(len(printerRates)) # 1 if operational, 0 if broken
    lastPrint = -1*np.ones(len(printerRates)) # Time of each printer's last print job
    while time < numDays:
        probs = np.append(printerRates*printers,vitalRate)
        overallRate = sum(probs)
        randNum1 = np.random.rand(1)[0]
        time -= np.log(randNum1)/overallRate
        probs = probs/overallRate
        randNum2 = np.random.rand(1)[0]
        while np.any(printers == 0) and np.sum(np.all([printers == 1,time - lastPrint >= printerLag],axis=0)) > 0:
            fixInd = np.where(printers == 0)[0][-1]
            printInd = np.where(np.all([printers == 1,time - lastPrint >= printerLag],axis=0))[0][0]
            printers[fixInd] = 1
            lastPrint[printInd] += 1
            del fixInd
            del printInd
        ind = np.where([randNum2 <= sum(probs[:ind + 1]) for ind in range(len(probs))])[0][0]
        if ind < len(printers):
            printers[ind] = 0
            if np.sum(np.all([printers == 1,time - lastPrint >= printerLag],axis=0)) > 0:
                printInd = np.where(np.all([printers == 1,time - lastPrint >= printerLag],axis=0))[0][0]
                lastPrint[printInd] = time
                printers[ind] = 1
                del printInd
        else:
            if np.any(np.all([printers == 1,time - lastPrint >= printerLag],axis=0)):
                printInd = np.where(np.all([printers == 1,time - lastPrint >= printerLag],axis=0))[0][0]
                lastPrint[printInd] = time
                del printInd
            else:
                break
        del ind
    times.append(time)
del numSim

print('Average Survival Time = ' + str(round(np.average(times),1)) + \
' +/- ' + str(round(np.std(times),1)) + ' days')
print('Probability of Survival = ' + str(round(100*sum(np.array(times) >= numDays)/len(times),1)) + '%')

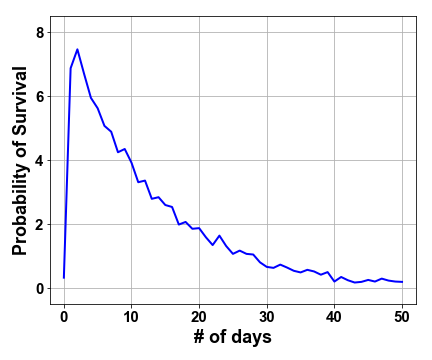
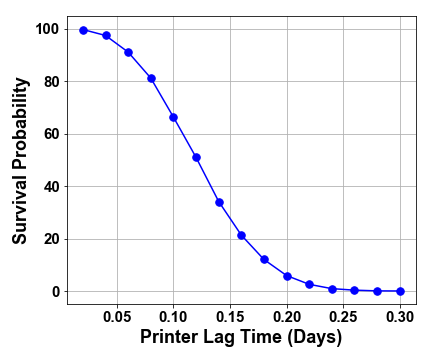This added stochasticity changes the entire game. We intrepid Riddler-nauts now have essentially a zero percent chance of surviving our martian journey with an average survival of \(13.2 \pm 12.6\) days. So what needs to change??? What do our highly-skilled RASA engineers need to focus on to get us to the 1825 day finish line? For starters, let’s pretend that the Riddler Nation Senate decided to approve funding for as many 5% printers as we need to have a 50% chance of survival (man, those senators love their coin flips). If that were the case, we would need seven printers instead of three, as seen in the second figure. But with space travel costing $1250 per pound at best, each printer weighing 50 pounds, and each printer costing $1500, the senators are starting to clamor about the extra $256K. Instead, they are encouraging us to optimize the three printers we already have. In the end, lowering the breaking probability of our printers won’t help much – even if the printers never break, it’s reasonably probable for more than three pieces of vital machinery to break in a single day and the lag between printing jobs will do us in. Sure enough, simulating this perfect-printer scenario produces an average survival of \(20.5 \pm 20.0\) days so we should definitely focus on reducing the rate-limiting 24 hour recharging period. In order to reach the 50% goal set by the Senate with our original three printers, we would need to lower the lag time to just under 3 hours as seen in the final figure.

This problem is a perfect example of how deterministic, average-based methods can sometimes be misrepresentative of the real scenario. These simpler methods told us that we had a fighting chance, but let’s be honest, malfunctions aren’t going to happen like clockwork. Only by accounting for the randomness and noise of the stochastic processes of the real world do we realize that something needs to change or we’re going to end up as martian toast. If anyone in Riddler Nation wants to mess around with the simulation or see if a different strategy would be more effective, the underlying code is available here. Safe travels, Riddler-nauts!!!