13 Oct 2018

Riddler Answer: Grazed and Confused

This week's Riddler asks us to provide some restraint for an overeating goat before they graze a farmer out of business...

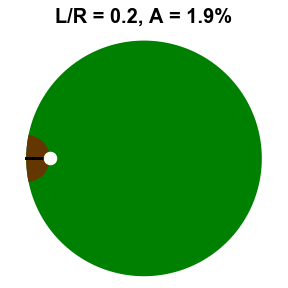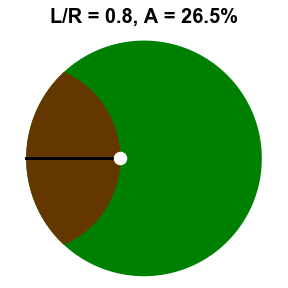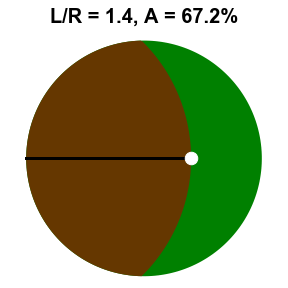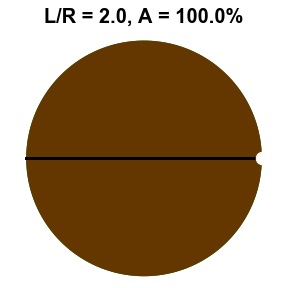On this week’s edition of the Riddler, Moritz Hesse introduces us to a farmer that owns a circular field of radius $R$ and a particularly hungry goat. Growing tired of the kid running amok, the farmer decides to tie the goat up to a post on the fence surrounding the field, but needs to ensure that the goat doesn’t graze the entire field. The question posed is this: How long does the goat’s tether need to be to ensure that the goat only eats half of the circular field? To better visualize this agricultural quandry, see the gif shown to the right. At shorter tether lengths, the more limiting factor is the actual tether restricting the goat from running free within the circle, but as it gets longer, the fence is really the only thing limiting the goat’s appetite.

Solution

To find the correct tether length, we really just need a bit of clever geometry. The grazing area covered by a tether of length $L$ can be split into two regions shown in the diagram to the right: the area swept out by the tether if the goat is pulling it taut, which we will call $A_1$ , and the pizza crust looking areas to the sides of the post that the goat is tied to, which we will call $A_2$ . Let’s start by focusing on $A_1$ and laying things out a bit more clearly. In the second diagram, I define $\theta$ as the angle from vertical that the goat can reach with a taut leash until hitting the fence. This can be calculated in terms of $R$ and $L$ as

$\theta = \cos^{-1}\frac{L/2}{R}.$

This quickly leads us to the area of $A_1$ as

$A_1 = \theta L^2.$

The area of $A_2$ is a bit more complicated, but I compared them to pizza crust for a reason. We can calculate $A_2$ by cutting out a slice of pizza out of the circular field of angle $\pi - 2\theta$ and subtracting away the cheesy triangular portion with all the toppings. This leads us to

$A_2 = (\pi/2 - \theta) R^2 - \frac{L}{2} R \sin \theta$

Finally, we can combine these areas to calculate the entire grazing area as

$A_g = A_1 + 2 A_2 = \theta L^2 + 2 \left[ (\pi/2 - \theta) R^2 - \frac{L}{2} R \sin \theta \right]$

Setting $A_g = \pi R^2$ and algebraically solving for $L$ would prove difficult/impossible so I decided to use a Nelder-Mead simplex algorithm to numerically solve for $L$ in the following Python script:

import numpy as np
from scipy.optimize import minimize

targetPortion = 0.5

def grazing_area(tether):
    global targetPortion
    ### Assuming field radius is 1 for ease of calculation ###
    theta = np.arccos(tether/2)
    area = (theta*(tether**2) + 2*((np.pi/2 - theta) - tether/2*np.sin(theta)))/np.pi
    return (area - targetPortion)**2

res = minimize(grazing_area,0.5,method='nelder-mead',tol=1e-6)
print(str(round(100*targetPortion,1))[:-2] + '% grazing at L = ' + str(round(res['x'][0],4)) + 'R')

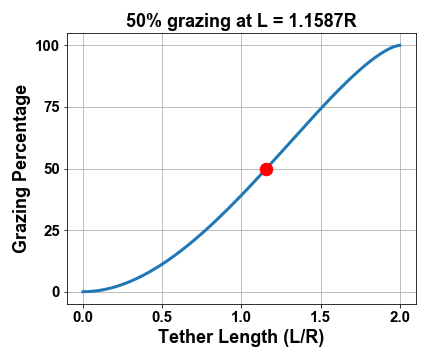This code advises us that in order to restrict the goat to half of the grazing area, we must tie up the ravenous kid with a tether of length $L = 1.1587R$ . In fact, just in case the local veterinarian recommends increasing or decreasing the goat’s diet, we can vary the target portion of the grazing area to produce the dependency as shown in the graph to the right. Hope this explanation was reasonably clear! Stay classy, Riddler Nation!